Plicker Questions from Class
Bayesian Inference
- What is the best definition for our p-value in probability notation?
-
\(\mathbb{P}\)(\(H_0\) is true data or more extreme) - \(\mathbb{P}\)(\(H_0\) is true)
-
\(\mathbb{P}\)(data or more extreme \(H_0\) is true) - \(\mathbb{P}\)(data)
-
Chapter 3
- Which of the following is an appropriate null hypothesis based on comparing Reed’s ethnicity to the state of Oregon’s ethnicity?
- Ethnic diversity and choice of college are independent of one another.
- Ethnic diversity and home-state are independent of one another.
- \(p_{asian} = p_{black} = p_{hispanic} = p_{white} = p_{other}\).
- The first-year class at Reed is sampled from a population that shares the same ethnic distribution as Oregon.
- Based on the problem setup with \(\hat{p} = 0.05\) and a sample size of 1002 resulting in a confidence interval of (0.0364, 0.0634), which of the following are appropriate claims to make about the population parameter p?
- We have evidence that less than 7% of all Americans are atheists.
- We have evidence that more than 4% of all Americans are atheists.
- We are certain it matches exactly with the sample proportion of 0.05.
- Two of the above are TRUE.
Chapter 2
- We are given that \(n = 1002\), \(\hat{p} = 0.05\). Which of the
below is the correct calculation of the 95% confidence interval?
- \[0.05 \pm 1.65 \sqrt{\dfrac{0.05 \times 0.95}{1002}}\]
- \[0.05 \pm 1.96 \left(\dfrac{0.05 \times 0.95}{\sqrt{1002}}\right)\]
- \[0.50 \pm 2.58 \sqrt{\dfrac{50 \times 952}{1002}}\]
- \[0.05 \pm 1.96 \sqrt{\dfrac{0.05 \times 0.95}{1002}}\]
- Based on the null distribution and the observed test statistic, what is our decision?
- Accept \(H_0\)
- Fail to reject \(H_a\)
- Reject \(H_a\)
- Reject \(H_0\)
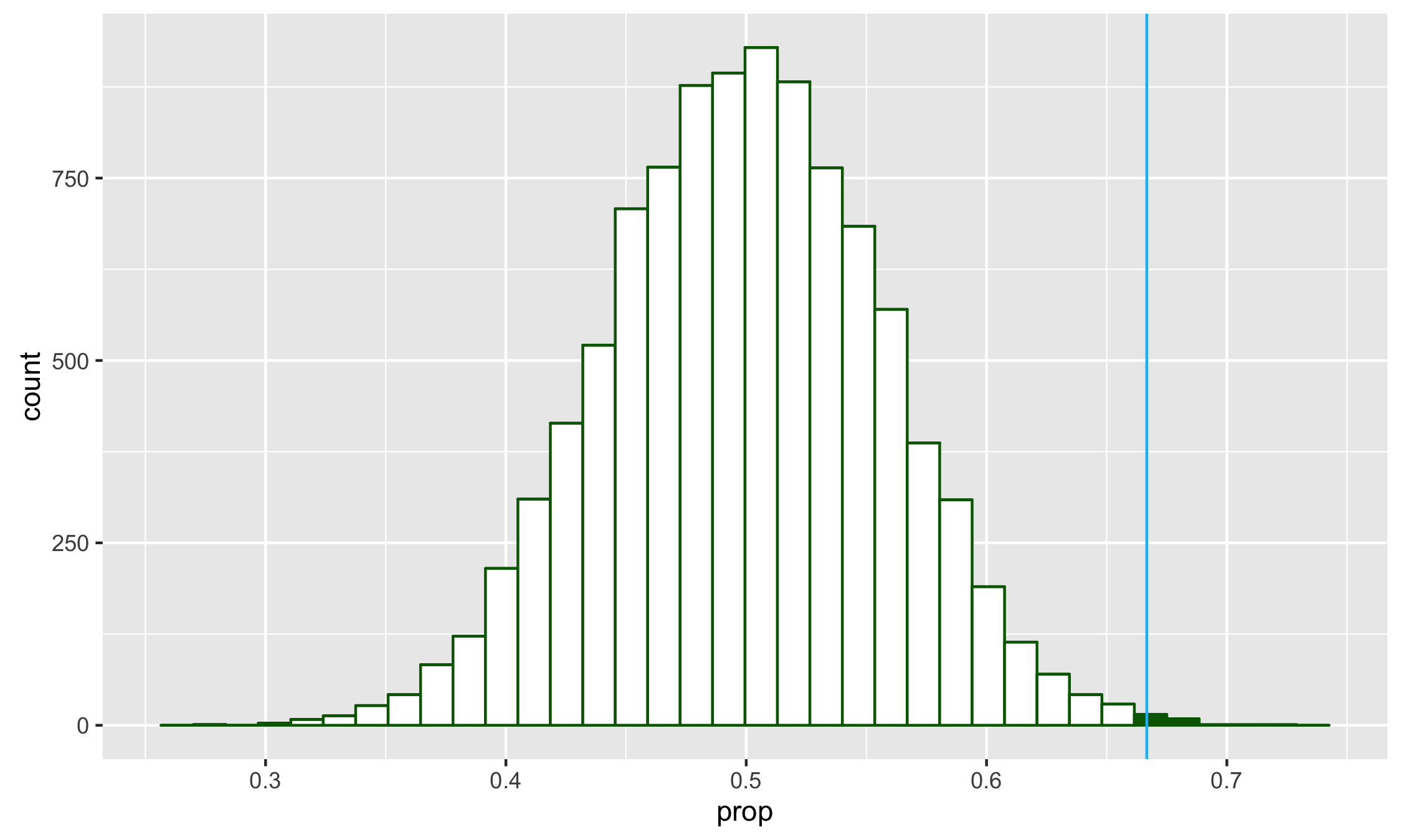
- What is the alternative hypothesis for this question trying to understand American adult views on gay marriage? Let \(p\) be the true proportion of Americans who favor same-sex marriage.
- \[H_a: p = 0.5\]
- \[H_a: p = 0.67\]
- \[H_a: p > 0.67\]
- \[H_a: p > 0.5\]
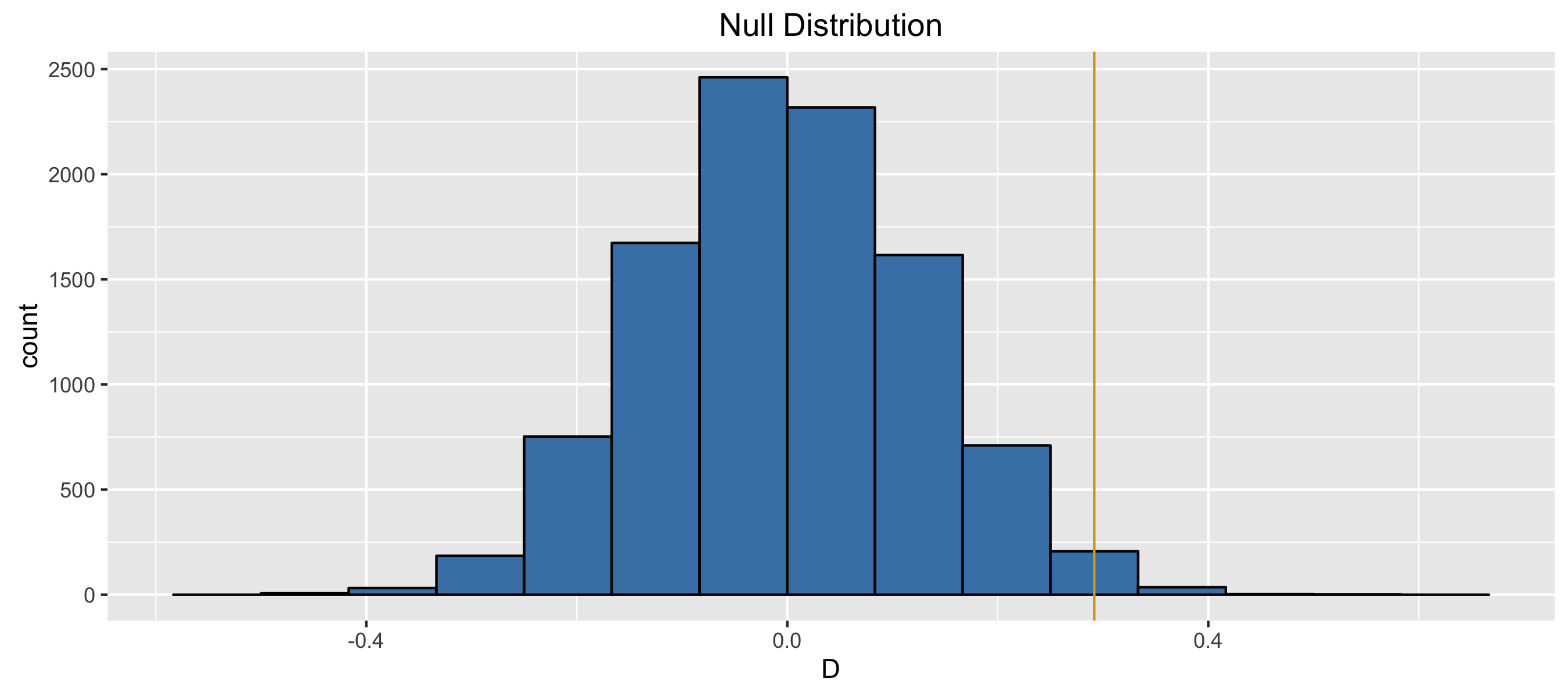
- Do the results of the simulation below based on 10,000 simulations provide convincing evidence of gender discrimination against women, i.e. dependence between gender and promotion decisions?
- No, the data do not provide convincing evidence for the alternative hypothesis, therefore we can’t reject the null hypothesis of independence between gender and promotion decisions. The observed difference between the two proportions was due to chance.
- Yes, the data provide convincing evidence for the alternative hypothesis of gender discrimination against women in promotion decisions. The observed difference between the two proportions was due to a real effect of gender.
Appendix A (Probability)
- Let \(Y \sim Bin(n, p)\). Using random variable identities, find \(\mathbb{E}(Y)\) and \(\mathbb{S}(Y) = SD(Y)\).
- \(np(1 - p)\); \(\sqrt{p(1 - p)}\)
- \(np\); \(\sqrt{np(1 - p)}\)
- \(np\); \(\sqrt{p(1 - p)}\)
- \(np\); \(\sqrt{(p^n)(1-p)^n}\)
- In the case of the bouncing ball, where X takes the value 1 if it bounces R (with prob p) and 0 if it bounces L, what is \(SD(X)\)?
- \[\sqrt{1 - 2p + p^2}\]
- \[\sqrt{p(1 - p)}\]
- \[(1-p)p\]
- \[\sqrt{1 - 2p + 2p^2}\]
- What is \(\mathbb{P}(Y = 3)\)?
- \[3(1-p)^3\]
- \[p^3\]
- \[p^3(1-p)\]
- \[4p^3(1-p)\]
- What is the standard deviation of your winnings if you bet 1 dollar but play 3 times?
- 1.73
- 2.99
- 8.97
- 2.96
- In playing the standard game of roulette, what are your expected winnings if you go back to betting 1 dollar but play the game 3 times?
- 2.85
- 0.95
- 1.90
- 8.55
- What is the standard deviation of your winnings if you triple your bet and play one game?
- 1.73
- 2.99
- 8.97
- 2.96
- The American Cancer Society estimates that about 1.7\% of women have breast cancer.
(http://www.cancer.org/cancer/cancerbasics/cancer-prevalence). Susan G. Komen For The Cure Foundation states that mammography correctly identifies about 78% of women who truly have breast cancer. (http://ww5.komen.org/BreastCancer/AccuracyofMammograms.html) An article published in 2003 suggests that up to 10\% of all mammograms result in false positives for patients who do not have cancer.
(http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1360940) When a patient goes through breast cancer screening there are two competing claims: patient had cancer and patient doesn’t have cancer. Suppose a woman who gets tested once and obtains a positive result wants to get tested again. In the second test, what should we assume to be the probability of this specific woman having cancer?
- 0.017
- 0.12
- 0.0133
- 0.88
- What is the probability that this woman has cancer if this second mammogram also yielded a positive result?
- 0.0936
- 0.088
- 0.48
- 0.52
- In the US population, 9% of people are left-handed and 15% of people have blue eyes. If you select an American at random, what is the probability they are right-handed and have blue eyes?
- 0.0135
- 0.24
- 0.1365
- None of the above
- Two fair dice are rolled. What is the probability that either the sum is 8 or that at least one of the dice comes up a 6?
- 11/36
- 14/36
- 15/36
- 16/36
- In a certain semester at some other university, 500 students enrolled in both Calculus I and Physics I. Of these students, 82 got an A in calculus, 73 got an A in physics, and 42 got an A in both courses. Which of the following probabilities is the smallest? The probability that a randomly chosen student. . .
- Got an A in at least one of the two courses
- Got an A in both of the two courses
- Got an A in calculus but not in physics
- Got an A in physics but not calculus
Chapter 1
- Which measure of spread would be LEAST sensitive to the presence of outliers?
- Standard Deviation
- IQR
- Range
- Depends on the dataset
- Which of these variables do you expect to be uniformly distributed?
- weights of adult females
- salaries of a random sample of people from Oregon
- birthdays of classmates (day of the month)
- Two of the above
- In a study reported in the Archives of Pediatric and Adolescent Medicine on treating warts, researchers investigated whether liquid nitrogen cryotherapy (“freezing it off”) or common duct tape would be a more effective treatment for kids with warts. The researchers randomly assigned the 51 patients to two treatment groups and found that 22 of 26 patients treated with duct tape saw complete disappearance of their warts, compared to 15 of 25 patients in the cryotherapy group. What are the observational units?
- Methods for wart removal
- Kids with warts
- Warts
- Researchers
- For the wart study, where researchers randomly assigned the 51 patients to two treatment groups and found that 22 of 26 patients treated with duct tape saw complete disappearance of their warts, compared to 15 of 25 patients in the cryotherapy group. What is the explanatory variable?
- Whether a wart completely disappeared or not
- The proportion of kids whose warts completely disappeared
- Which treatment (cryotherapy or duct tape) was used on each subject
- Whether or not cryotherapy and duct tape are equally effective in removing warts on kids
- In a study on treating warts, researchers investigated whether cryotherapy or common duct tape would be a more effective treatment for kids with warts. The 51 patients were randomly assigned to two treatment groups and found that 22 of 26 patients treated with duct tape saw complete disappearance of their warts, compared to 15 of 25 patients using cryotherapy. Assuming the results were statistically significant (p<0.05), would it be correct to conclude that duct tape caused more warts to disappear than did cryotherapy?
- No, there could be a confounding variable.
- No, cause-and-effect can only be concluded from observational studies.
- Yes, the data clearly show an association between the treatment group and the complete disappearance of warts.
- Yes, this is a randomized experiment.
- In a study on treating warts, researchers investigated whether liquid nitrogen cryotherapy (“freezing it off”) or common duct tape would be a more effective treatment for kids with warts. The researchers randomly assigned the 51 patients to two treatment groups and found that 22 of 26 patients treated with duct tape saw complete disappearance of their warts, compared to 15 of 25 patients in the cryotherapy group. Was this study double–blind?
- No, the kids could tell which treatment group they were in.
- Yes, the students were randomly assigned to groups so double--blind is implied.
- Yes, the researchers did not know which treatment was being applied.
- There is not enough information given to decide.
- Match the definition with its correct term: The target group about which you’d like to make inferences
- Sample
- Population
- Summary statistic
- Anecdote
- Match the definition with its correct term: The individual unit on which you make observations
- Parameter
- Sample
- Case
- Census