class: center, middle, inverse, title-slide # <code>infer</code> ## An R package for tidy statistical inference <br><br> ### Dr. Chester Ismay <br> Data Science Curriculum Lead at DataCamp <br> GitHub: <a href="https://github.com/ismayc">ismayc</a> <br> Twitter: <a href="https://twitter.com/old_man_chester">@</a><a href="https://twitter.com/old_man_chester">old_man_chester</a> ### 2018-01-27 (R User Day at Data Day Texas) <br><br> Slides available at <a href="http://bit.ly/infer-austin" class="uri">http://bit.ly/infer-austin</a> <br> Package webpage at <a href="https://infer.netlify.com" class="uri">https://infer.netlify.com</a> --- layout: true .footer[Slides available at <http://bit.ly/infer-austin> <br> Package webpage at <https://infer.netlify.com>] --- ## Understanding who you are - Who uses hypothesis testing/confidence intervals at least once a week? -- - Who uses the `tidyverse` at least once a week? -- - Who has heard of permutation testing? - Randomization-based methods? - Resampling methods? - Bootstrap methods? --- ## Pre-requisites for this talk - Some experience with statistical inference (hypothesis testing / confidence intervals) -- - A ~~admiration~~, ~~abundance of love~~, ~~won't do anything without it~~ respect for the `tidyverse` and its power to get more users into doing data analysis/visualization quickly - The pit of success -- - ~~Ability~~ Desire to think differently about statistical inference using computational methods as the driver --- class: center ### Is this statistical inference to you? [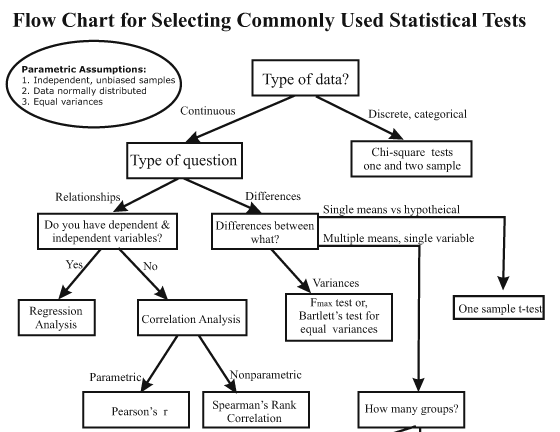](https://i.pinimg.com/originals/e5/ea/32/e5ea322d61bd36a5062080b1b5fe6daa.gif) --- class: middle <small>Students at Virginia Tech studied which vehicles come to a complete stop at an intersection with four-way stop signs, selecting at random the cars to observe. <!--They looked at several factors to see which (if any) were associated with coming to a complete stop. (They defined a complete stop as “the speed of the vehicle will become zero at least for an [instant]”). Some of these variables included the age of the driver, how many passengers were in the vehicle, and type of vehicle.--> The <font color="purple">explanatory</font> variable used here is the arrival position of vehicles approaching an intersection all traveling in the same direction. They classified this arrival pattern into three groups: whether the vehicle arrives alone (<font color="purple"><code><small>single</small></code></font>), is the <font color="purple"><code><small>lead</small></code></font> in a group of vehicles, or is a <font color="purple"><code><small>follow</small></code></font>er in a group of vehicles. Is there an association between <font color="purple">arrival pattern</font> and whether a <font color="darkgreen"><code><small>complete</small></code></font> stop or <font color="darkgreen"><code><small>not_complete</small></code></font> was made?</small> <!--The students studied one specific intersection in Northern Virginia at a variety of different times. Because random assignment was not used, this is an observational study. Also note that no vehicle from one group is paired with a vehicle from another group.--> <br> <tiny>- From <a href="http://math.hope.edu/isi/"> "Introduction to Statistical Investigations" </a> by Tintle et al.</tiny> --- class: middle Which type of hypothesis test should we conduct here? - A. Independent samples t-test - B. One proportion test - C. Chi-Square test of independence - D. ANOVA --- ```r library(tidyverse) # https://ismayc.github.io/talks/data-day-texas-infer/car_stop.rds download.file("http://bit.ly/car_stop_rds", destfile = "car_stop.rds") car_stop <- read_rds("car_stop.rds") car_stop %>% sample_n(10) ``` ``` # A tibble: 10 x 2 stop_type vehicle_type <chr> <chr> 1 complete single 2 complete follow 3 complete lead 4 complete single 5 not_complete follow 6 not_complete lead 7 complete single 8 complete follow 9 complete single 10 complete lead ``` --- class: middle Which type of hypothesis test should we conduct here? - A. Independent samples t-test - B. One proportion test - C. Chi-Square Test of Independence - D. ANOVA -- <br> *** ## Answer: - **C. Chi-Square Test of Independence** --- class: middle ## Let's do this in R - Using a `data` argument ```r chisq.test(data = car_stop, x = stop_type, y = vehicle_type) ``` -- ``` Error in chisq.test(data = car_stop, x = stop_type, y = vehicle_type) ``` -- - Using a formula ```r chisq.test(data = car_stop, formula = vehicle_type ~ stop_type) ``` -- ``` Error in chisq.test(data = car_stop, formula = vehicle_type ~ stop_type) ``` <br> --- ## Finally ```r chisq.test(car_stop$stop_type, car_stop$vehicle_type) ``` ``` Pearson's Chi-squared test data: car_stop$stop_type and car_stop$vehicle_type X-squared = 3.9476, df = 2, p-value = 0.1389 ``` --- ## ```r ?chisq.test() ``` [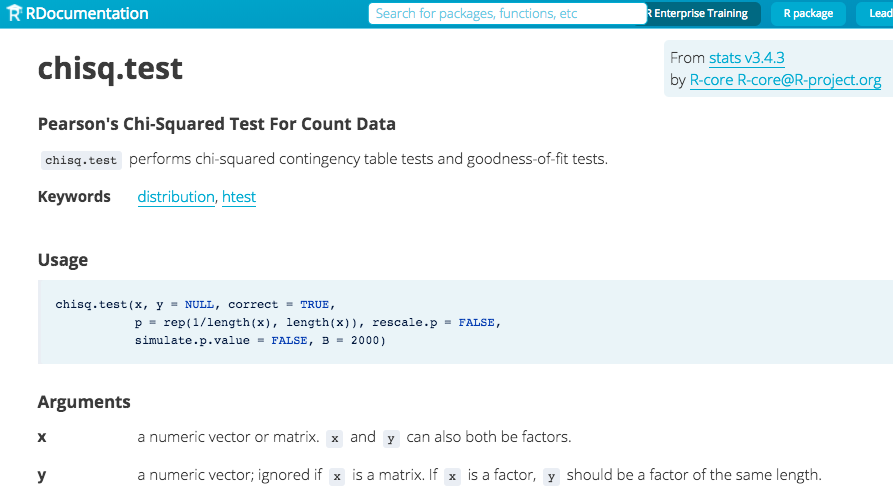](https://www.rdocumentation.org/packages/stats/versions/3.4.3/topics/chisq.test) --- <img src="slide_deck_files/figure-html/unnamed-chunk-9-1.png" width="1008" /> P-value is 0.1389. --- Is there an association between arrival pattern and whether or not a complete stop was made? ## The null hypothesis -- > No association exists between the arrival vehicle's position and whether or not it makes a complete stop. ## The alternative hypothesis -- > An association exists between the arrival vehicle's position and whether or not it makes a complete stop. --- ## How can computation help us to understand what is going on here? -- [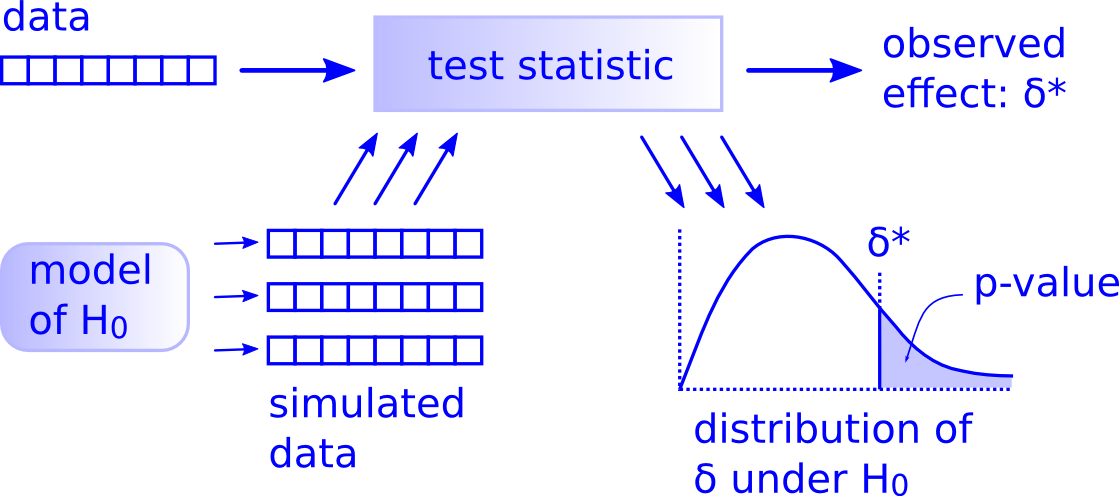](http://allendowney.blogspot.com/2016/06/there-is-still-only-one-test.html) --- ## The tricky step -- Modeling the null hypothesis - How do we simulate data assuming the null hypothesis is true in our problem (there is no association between the variables)? -- - What might the sample data look like if the null was true? --- ### Properties of the original sample collected ```r car_stop %>% count(stop_type, vehicle_type) ``` ``` # A tibble: 6 x 3 stop_type vehicle_type n <chr> <chr> <int> 1 complete follow 76 2 complete lead 38 3 complete single 151 4 not_complete follow 22 5 not_complete lead 5 6 not_complete single 25 ``` -- ```r ( orig_table <- car_stop %>% janitor::tabyl(stop_type, vehicle_type) ) ``` ``` stop_type follow lead single complete 76 38 151 not_complete 22 5 25 ``` --- ### Permute the sample data ``` # A tibble: 317 x 2 stop_type vehicle_type <fct> <fct> 1 complete follow 2 not_complete follow 3 complete follow 4 not_complete single 5 complete single 6 not_complete follow 7 not_complete single 8 complete follow 9 not_complete lead 10 complete lead # ... with 307 more rows ``` -- ``` stop_type follow lead single complete 79 35 151 not_complete 19 8 25 ``` --- ## Comparing the original and permuted sample ```r orig_table %>% janitor::adorn_totals(where = c("row", "col")) ``` ``` stop_type follow lead single Total complete 76 38 151 265 not_complete 22 5 25 52 Total 98 43 176 317 ``` ```r new_table %>% janitor::adorn_totals(where = c("row", "col")) ``` ``` stop_type follow lead single Total complete 79 35 151 265 not_complete 19 8 25 52 Total 98 43 176 317 ``` --- ## Where are we? [](http://allendowney.blogspot.com/2016/06/there-is-still-only-one-test.html) --- ## Test statistic - Chi-square test statistic ([Wikipedia](https://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test)) - Measure of how far what we observed in our sample is from what we would expect if the null hypothesis was true -- ```r chisq.test(car_stop$stop_type, car_stop$vehicle_type)$statistic ``` ``` X-squared 3.947648 ``` --- ## For the permuted data ```r chisq.test(perm1$stop_type, perm1$vehicle_type)$statistic ``` ``` X-squared 1.408986 ``` -- ## Another permutation ```r chisq.test(perm2$stop_type, perm2$vehicle_type)$statistic ``` ``` X-squared 0.3604528 ``` --- ## What does the distribution of multiple repetitions of the permuted data look like? ``` # A tibble: 1,000 x 2 replicate stat <fct> <dbl> 1 1 1.05 2 2 7.24 3 3 0.253 4 4 2.16 5 5 1.60 6 6 3.95 7 7 1.94 8 8 1.68 9 9 0.242 10 10 3.26 # ... with 990 more rows ``` --- <small>The distribution of multiple repetitions of the permuted data</small> -- <img src="slide_deck_files/figure-html/unnamed-chunk-20-1.png" width="1008" /> -- <small>Recall the traditional method using the Chi-square distribution </small> <img src="slide_deck_files/figure-html/unnamed-chunk-21-1.png" width="1008" /> --- <!-- So how did I generate this code to permute? --> ## Objectives of `infer` - Implement common classical inferential techniques in a `tidyverse`-friendly framework that is expressive of the underlying procedure. -- - Dataframe in, dataframe out - Compose tests and intervals with pipes - Unite computational and approximation methods - Reading a chain of `infer` code should describe the inferential procedure --- class: inverse, center, middle # The `infer` verbs ---  --- 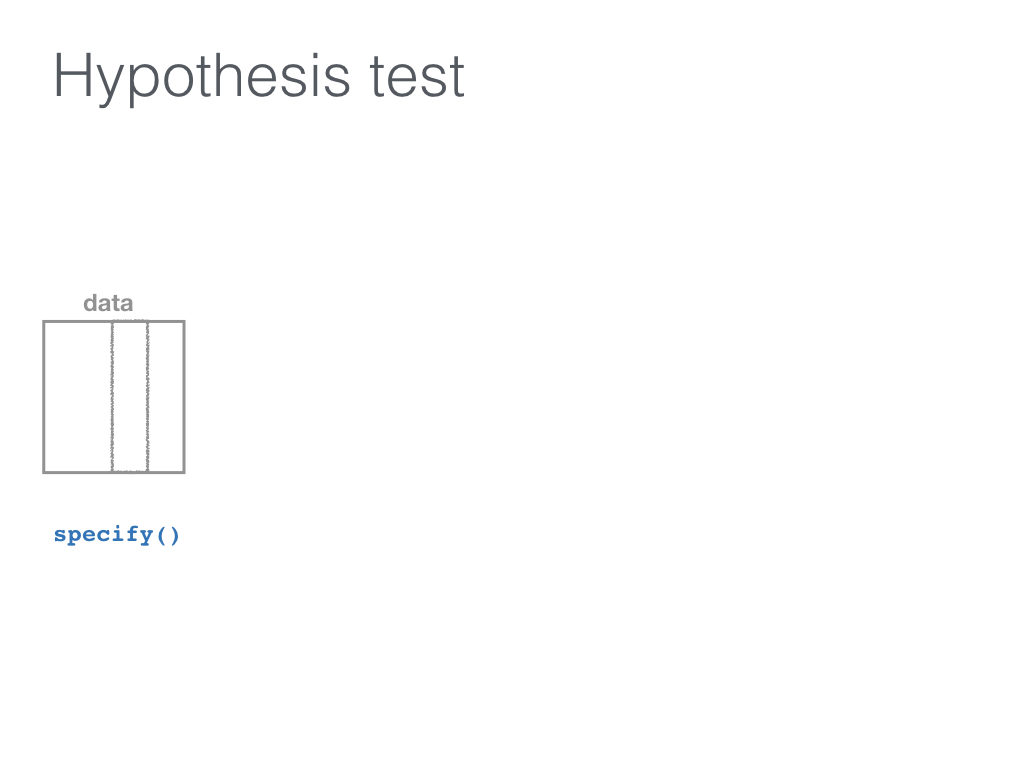 ---  ---  ---  ---  ---  --- 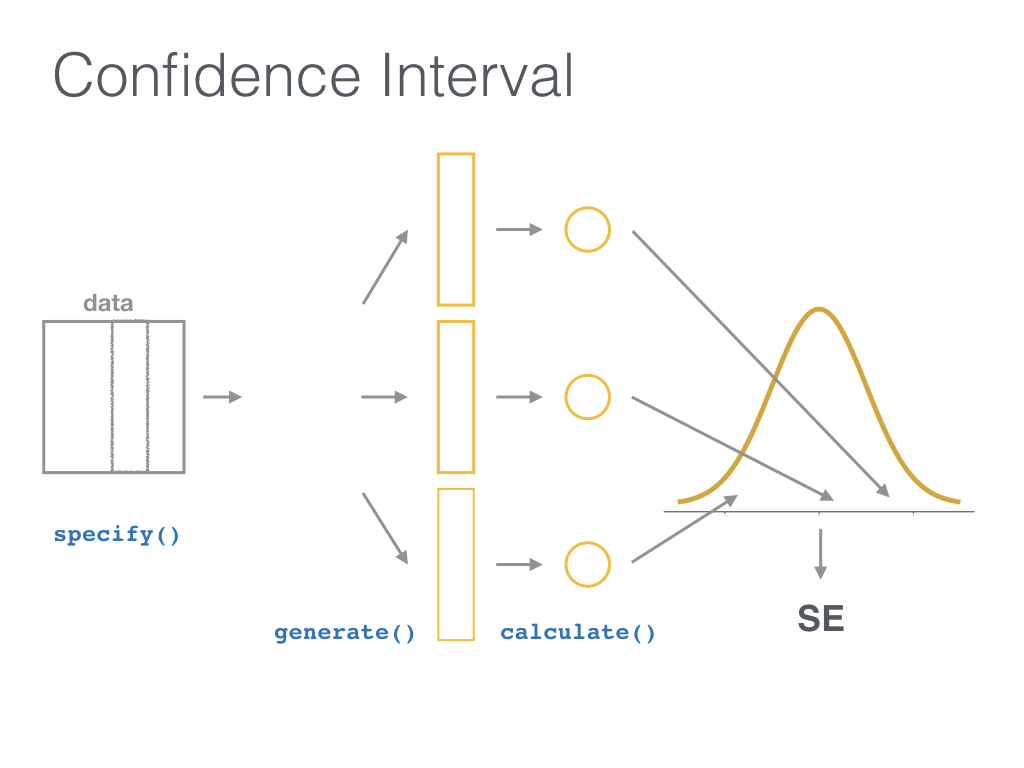 ---  ---  ---  --- ```r car_stop %>% specify(stop_type ~ vehicle_type) %>% hypothesize(null = "independence") %>% generate(reps = 1000, type = "permute") %>% calculate(stat = "Chisq") ``` ``` # A tibble: 1,000 x 2 replicate stat <fct> <dbl> 1 1 0.509 2 2 0.760 3 3 1.79 4 4 1.83 5 5 0.525 6 6 4.74 7 7 1.11 8 8 2.51 9 9 1.11 10 10 0.421 # ... with 990 more rows ``` --- ## Back to the example ```r car_stop %>% specify(stop_type ~ vehicle_type) %>% hypothesize(null = "independence") %>% generate(reps = 1000, type = "permute") %>% calculate(stat = "Chisq") %>% visualize() ``` <img src="slide_deck_files/figure-html/unnamed-chunk-23-1.png" width="1008" /> --- ## What's to come - Wrapper functions: `t_test`, `chisq_test`, etc. - Generalized input to `calculate()` - For example, `calculate(trimmed_mean)` - Support for more advanced regression models - Adding features to `visualize()` - Show both traditional and computation methods - Implement list-columns in the `generate()` step --- ## Tips and tricks for package development - Use [GitHub](https://github.com/andrewpbray/infer/) and pull requests to the `master` branch - [Create useful vignettes](https://cran.r-project.org/web/packages/infer/vignettes/flights_examples.html) so others know how your pkg works - Write tests and assertions for your code - [Buy and read Richie's *Testing R Code* book](https://www.crcpress.com/Testing-R-Code/Cotton/p/book/9781498763653) - Let [travis-ci](https://travis-ci.org/andrewpbray/infer) do [the work](https://github.com/andrewpbray/infer/blob/master/.travis.yml) for you - Use Hadley's [`pkgdown` package](https://github.com/r-lib/pkgdown) to build a pkg website - Host it on Netlify.com to be super cool --- ## More info - https://infer.netlify.com - Many examples under Articles there with more to come - Plans to be implemented in [www.ModernDive.com](www.ModernDive.com) by this summer - [Sign up](http://eepurl.com/cBkItf) for the ModernDive mailing list for details - Two DataCamp courses currently launched that use `infer` - [Inference for Numerical Data](https://www.datacamp.com/courses/inference-for-numerical-data) by Mine Cetinkaya-Rundel - [Inference for Regression](https://www.datacamp.com/courses/inference-for-linear-regression) by Jo Hardin - Two more DataCamp courses to be launched --- layout: false class: middle - Special thanks to [Andrew Bray](https://andrewpbray.github.io) and the other pkg contributors - Slides created via the R package [xaringan](https://github.com/yihui/xaringan) by Yihui Xie - Slides available at <http://bit.ly/infer-austin> - Source code for these slides at <https://github.com/ismayc/talks/tree/master/data-day-texas-infer> <br> <center> <a href="https://giphy.com/gifs/wMY3LjQQMqo5W?utm_source=media-link&utm_medium=landing&utm_campaign=Media%20Links&utm_term="> <img src="peele.gif" style="width: 550px;"/> </a> </center>